
En informatique, les opérations logiques sont nécessaires car elles peuvent être utilisées pour modéliser la manière dont les informations circulent dans les circuits électriques, tels que les circuits à l'intérieur d'une CPU. Ces types d'opérations sont appelés opérations booléennes.
Les éléments d'un circuit qui se comportent selon la logique booléenne sont appelés des portes logiques.
Opérations logiques fondamentales
Les sept opérations logiques suivantes prennent des entrées vraies (1) ou fausses (0) et produisent une seule valeur de sortie également vraie ou fausse.
La plupart de ces opérations peuvent prendre plus de deux entrées, à l'exception de l'opération NOT qui ne prend qu'une entrée. Vous trouverez ci-dessous des exemples utilisant seulement une ou deux entrées, ce qui se passe généralement à l’intérieur d’un ordinateur.
Les opérations sont énumérées ci-dessous. Cliquez sur un lien pour une opération pour en savoir plus.
- ET
- OU
- NE PAS
- NAND
- NI
- XOR
- XNOR
L'opération logique AND ne renvoie vrai que si toutes ses entrées sont vraies. Si l'une des entrées est fausse, la sortie est également fausse.
En programmation informatique, l'opération AND est généralement écrite sous la forme && (deux esperluettes).
En algèbre booléenne, l'opération AND de deux entrées A et B peut être écrite sous la forme AB .
Vous trouverez ci-dessous la table de vérité pour une opération AND à deux entrées et le schéma de circuit d'une porte logique AND.

| ET | ||
|---|---|---|
UNE | B | UN B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
OU
L'opération logique OU renvoie vrai si l'une de ses entrées est vraie. Si toutes les entrées sont fausses, la sortie est également fausse.
En programmation informatique, l’opération OR s’écrit généralement sous la forme || (deux barres verticales).
En algèbre booléenne, la valeur OU de deux entrées A et B peut être écrite sous la forme A + B.
Remarque: Ne confondez pas l'opération OU avec l'ajout arithmétique, même s'ils utilisent tous les deux le symbole " + ". Ce sont des opérations distinctes.
Vous trouverez ci-dessous la table de vérité pour une opération OU à deux entrées et le schéma de circuit d'une porte logique OU.

| OU | ||
|---|---|---|
UNE | B | A + B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
NE PAS
L'opération logique NOT renvoie true si son entrée est false et false si son entrée est true.
En programmation informatique, l'opération NOT est habituellement écrite sous la forme ! (un point d'exclamation).
En algèbre booléenne, la valeur NOT d'une entrée A peut être écrite sous la forme A (A avec un surcouple).
Vous trouverez ci-dessous la table de vérité pour une opération NOT et le schéma de circuit d'une porte logique NOT.

NAND
L'opération logique NAND (qui signifie "NOT AND") renvoie vrai si l'une de ses entrées est fausse, et faux si toutes ses entrées sont vraies.
En algèbre booléenne, la valeur NAND de deux entrées A et B peut être écrite sous la forme

NAND a la particularité d'être l'une des deux portes logiques "universelles" car toute autre opération logique peut être créée en utilisant uniquement des portes NAND. (L'autre porte logique universelle est NOR.)
Vous trouverez ci-dessous la table de vérité pour une opération NAND à deux entrées et le schéma de circuit d'une porte logique NAND.

| NAND | ||
|---|---|---|
UNE | B | ___ UN B |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NI
L'opération logique NOR (qui signifie "NOT OR") renvoie vrai si toutes ses entrées sont fausses et faux si l'une de ses entrées est vraie.
En algèbre booléenne, la valeur NOR des deux entrées A et B peut être écrite sous la forme
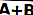
NOR a la particularité d'être l'une des deux portes logiques "universelles", car toute autre opération logique peut être créée en utilisant uniquement des portes NOR. (L'autre porte logique universelle est NAND.)
Vous trouverez ci-dessous la table de vérité pour une opération NOR à deux entrées et le schéma de principe d'une porte logique NOR.

| NI | ||
|---|---|---|
UNE | B | _____ A + B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
L'opération logique XOR (qui signifie "OU exclusif" renvoie vrai si l'une de ses entrées diffère, et faux si elles sont toutes identiques. En d'autres termes, si ses entrées sont une combinaison de vrai et de faux, la sortie de XOR est true: si toutes ses entrées sont vraies ou toutes fausses, la sortie de XOR est fausse.
En algèbre booléenne, la valeur XOR de deux entrées A et B peut être écrite sous la forme A⊕B . (Le symbole XOR,, ressemble à un signe plus dans un cercle.)
Voici la table de vérité pour une opération XOR à deux entrées et son schéma de circuit:

| XOR | ||
|---|---|---|
UNE | B | A⊕B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
L'opération logique XNOR (qui signifie "Exclusive NOT OR") renvoie true si toutes ses entrées sont identiques, et false si l'une d'entre elles diffère. En d'autres termes, si ses entrées combinent true et false, la sortie de XNOR est faux Si ses entrées sont toutes vraies ou toutes fausses, la sortie de XNOR est vraie.
En algèbre booléenne, la valeur XNOR de deux entrées A et B peut être écrite sous la forme

Vous trouverez ci-dessous la table de vérité pour une opération XNOR à deux entrées et son schéma de circuit:

| XNOR | ||
|---|---|---|
UNE | B | _____ A⊕B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
- Comment créer un programme informatique?
Accumulateur, Booléen, Idempotence, Opérateur, Termes de programmation
